Gitara to moja ulubiona zabawka. Prawdę pisząc mam wrażenie, że jest to na tyle doskonała zabawka, że nie potrzebuję już innych zabawek. Jest w tym prosto skonstruowanym przedmiocie coś genialnego. Sześć stalowych strun naciągniętych na deskę z progami, których odległości zmieniają się w sposób logarytmiczny. Z powodów natury matematycznej jest zupełnie niemożliwe by gitara się znudziła. Liczba możliwych kombinacji związanych z komponowaniem progresji akordów i skal jest praktycznie nieskończona – ok – przynajmniej na tyle duża, że nie może starczyć jednego życia na nawet pobieżne eksplorowanie gitarowego świata.
Gdy coś zaczyna brzmieć naiwnie i banalnie bierzemy bardziej zakręconą harmonię lub coś zmieniamy w używanej skali. W naszej otoczeniu kulturowym szczęśliwą liczbą jest siódemka. Ma to jakieś odbicie w muzyce. Skale diatoniczne i ich modusy składają się z siedmiu dźwięków. Dodanie do skali ósmego tonu zdecydowanie zwiększa bogactwo brzmieniowe. Daje też możliwości budowania harmonii, które brzmią mniej konformistycznie.
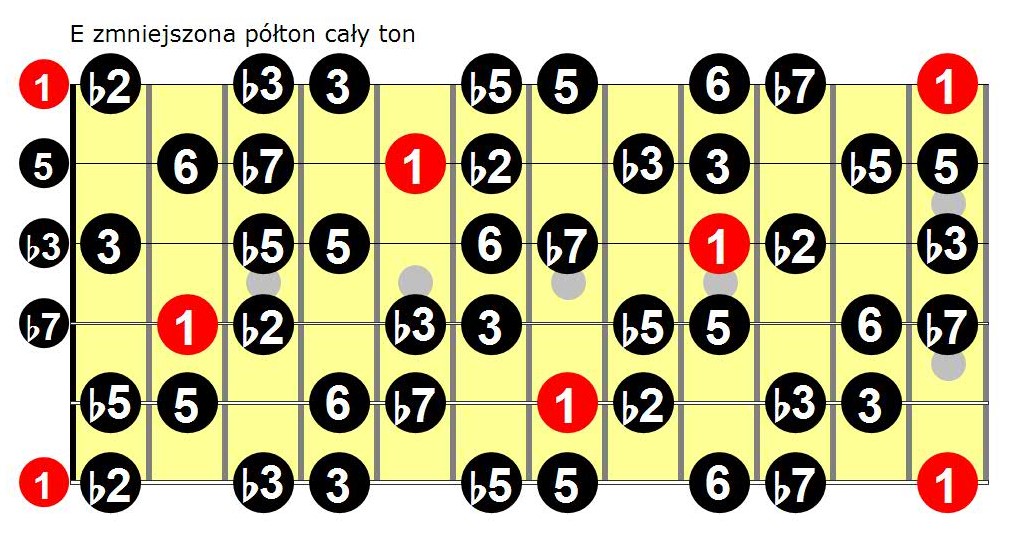
Dzisiaj ogrywamy skalę oktatoniczną – zmniejszoną pół ton cały ton. Zacznijmy nietypowo od zaprezentowania jej na gryfie gitary. Piękne, nieprawdaż?
Na początek proponuje to ogrywać bardzo powoli (jak wszystko na początek) – wsłuchać się i zauważyć dziwaczną konfigurację uczuć, które produkuje ten zestaw dźwięków. Dodajmy do tego odpowiednio gustowną progresję akordów. Poproś by kolega podegrał np: E7#9, C#7#9, G7 w tempie około 80 bitów na minutę. Akord nonowy dominantowy alterowany E7#9 opisywałem tutaj. I jak? Muzyka potrafi wygenerować dowolny zestaw uczuć. Dla mnie E7#9, C#7#9, G7 + skala zmniejszona opisuje unikalne wrażenie towarzyszące … awarii fiata Multipla.
Jaka jest genealogia skali oktatonicznej zmniejszonej półton cały ton? Jest to suma logiczna dwu akordów septymowych zmniejszonych: Edim7 + Fdim7. Łącznie daje to zestaw dźwięków pokazanych na powyższym obrazku. Warto sprawdzić osobiście jak się tu układa. Oczywiście taka progresja Edim7, Fdim7 stanowi też możliwy akompaniament do improwizacji w tej skali (jeśli tylko jesteś w stanie to ścierpieć). Są jednak łagodniejsze możliwości. Jak widać na powyższym gryfie w oparciu o skalę zmniejszoną można budować bardzo różnorodne harmonie.
Skala zmniejszona oktatoniczna jest intensywnie wykorzystywana w muzyce jazzowej i rocku progresywnym. Była znana od dawna w tradycyjnej muzyce perskiej. Zaś w naszym kręgu kulturowym pojawiła się w początkach XX wieku poprzez twórczość Mikołaja Rimskiego-Korsakowa. Sporadycznie była wcześniej stosowana przez dziewiętnastowiecznych klasyków. Ludwik van Beethoven w sonacie fortepianowej nr 11 B-dur op. 22. umieścił pasaż, który dla leniwego ucha brzmi jakby dysonansowo:
W powyższych taktach widzimy użycie skali zmniejszonej oktatonicznej. Niektórzy uważają, że jest to koronne dzieło fortepianowe Beethovena. Nie wiem. Zapewne nie chodzi o te kilka taków. Zachęcam do posłuchania bo z pewnością jest to dzieło bardzo niebanalne. Skoro tej skali używali klasycy to też możemy sobie poużywać na gitarze. Czego Wszystkim i sobie życzę!


Witam. A jak przedstawiałyby się akordy zbudowane na poszczególnych stopniach tej skali?
Pozdrawiam.
Moja propozycja wygląda tak: E7#9, Fdim7, G7#9, G#dim7, A#7#9, Hdim7, C#7#9, Ddim7. Z tego zestawu można losować cokolwiek w przypadkowej kolejności. Brzmi to interesująco niedorzecznie wraz ze skalą oktatoniczną H-W.
Czyli akordy septymowe budowane tercjowo na kolejnych stopniach skali, jeśli się nie mylę?
Np. E7#9 nie jest do końca akordem tercjowym bo pomiędzy septymą i noną zwiększoną mamy kwartę. Zaś Fdim7 jest tercjowy bo pomiędzy kolejnymi dźwiękami tego akordu są tercje małe. W ogólności skala oktatoniczna ma różnorodne możliwości harmonizacji i można ją harmonizować w sposób bardziej pogodny niż ta moja zakręcona propozycja.
Dziękuję za odpowiedź. Wg mnie całkiem „dorzecznie” to brzmi. Pozdrawiam!