Muzyka jest jest budownictwo okrętowe. Ignorowanie sztywnych zasad matematyki grozi zatonięciem. Z drugiej zaś strony te same matematyczne zasady pozwalają na budowę pięknych żaglowców.  Tak samo jest w muzyce, która od czasów Pitagorasa jest działem matematyki stosowanej, co chyba najłatwiej zobaczyć kontemplując układ progów  na gryfie gitary. Odległości kolejnych progów znajdują się w proporcji określonej przez pierwiastek dwunastego stopnia z 2 (samo patrzenie na gryf gitary napełnia mnie dziwnym spokojem związanym z obserwowanym porządkiem). Dzięki matematycznemu podejściu możemy dotrzeć w obszary brzmieniowe do których wyobraźnia by nas nigdy nie zaprowadziła.

Historycznych przykładów jest wiele. „Das Wohltemperierte Klavier” to dwa cykle 48 preludiów skomponowanych przez Bacha we wszystkich tonacjach dur i mol. Oczywiście dobrze nastrojony klawesyn nie jest nastrojony w znanym nam nudnym stroju równomiernie temperowanym lecz w tzw.  „Kirnberger III” opracowanym przez Johanna Philippa Kirnbergera (1721-1783). Tu nie chodzi tylko o geniusz kompozytorski Bacha ale też o kompletną prezentację zbioru częstotliwości zaproponowanych przez Kirnbergera. Jaki zresztą inny powód miałby Bach aby obchodzić koło kwintowej dwa razy nie pomijając np. C#dur itp???

Dopijam więc niedzielną poranną kawę i staram się wczuć w tą matematyczną kompletność. Plan na ten niedzielny poranek jest następujący: interesują nasz wszystkie muzyczne skale siedmiotonowe, w których półtony ze sobą nie sąsiadują. Skale takie nazywamy ankohemitonicznymi (po polsku bez-współ-półtonowymi). To podejście ma dwie cechy. Po pierwsze jest bardzo konserwatywne bo wyklucza bluesa i jazz czyli chyba najistotniejsze odkrycia muzyczne XX wieku. Z drugiej jednak strony wydaje się, że nawet większość zawodowych muzyków nie zdaje sobie sprawy, że w ramach tego ograniczenia mamy świat brzmieniowy znacznie bogatszy niż tylko skale diatoniczne i harmoniczne. Dokładnie istnieją aż 504 takie skale.

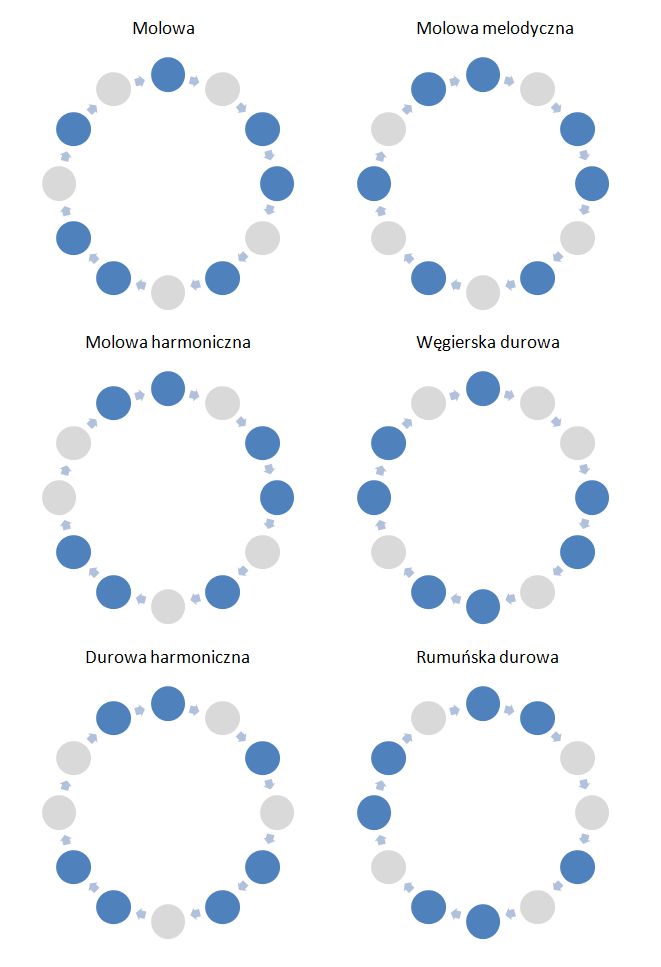
OK. To teraz odrobina matematyki. Nie będzie wzorów tylko obrazki. Mamy dwanaście różnych dźwięków w ramach skali chromatycznej. Ten o oktawę wyżej utożsamiamy z pierwszym. Dlatego przedstawiamy je jako taki zamknięty okrąg. Teraz pytanie jest następujące. Na ile sposobów można wybrać siedem dźwięków tak by półtony ze sobą nie sąsiadowały? Po chwili zabawy łatwo zauważyć, że istnieje tylko sześć możliwości. Pozostałe uzyskujemy przez obrót całego koła.

Postarajmy się teraz zidentyfikować te zbiory dźwięków ze znaną nam tradycją muzyczną.

1. Pierwsze koło to skala diatoniczna w jej siedmiu odmianach modalnych. To nie jest szczególnie egzotyczne dla osób z kręgu kulturowego muzyki zachodniej.
   • jońska (durowa)
   • dorycka
   • frygijska
   • lidyjska
   • miksolidyjska
   • eolska (molowa)
   • lokrycka
2. Drugie koło to skala molowa melodyczna i jej modusy. Tu już mamy nieco egzotyki i mniej uczęszczane obszary brzmieniowe:
   • mol melodyczna
   • dorycka b2
   • lidyjska zwiększona
   • lidyjska dominantowa
   • miksolidyjska b6
   • semilokrycka
   • superlokrycka

Prawdę pisząc grałem tylko w mol melodycznym i skali lidyjskiej dominantowej (którą bardzo polecam).

1. Trzecie koło to skala molowa harmoniczna, która zawiera już trzy półtony. Skala ta daje charakterystyczne brzmienie muzyki klasycznej a niektóre jej modusy są dobrze znane:
   • mol harmoniczna
   • lokrycka #6
   • jońska zwiększona
   • rumuńska molowa
   • frygijska dominantowa
   • lidyjska #2
   • ultralokrycka

Każdy kto bawi się gitarą dłużej niż kilka lat z pewnością grał w: mol harmonicznym, skali frygijskiej dominantowej (skala flamenco). Zdarzyło mi się też improwizować w skali rumuńskiej molowej.

1. Czwarte koło to skala węgierska durowa. Tutaj już pojawia się coś zupełnie dla mnie nowego. Bardzo ciekawe brzmienia i harmonie. Skala węgierska durowa i jej modusy zasługują na cykl osobnych wpisów blogowych. Może zauważmy tylko, że skala zaczyna się od tercji małej a potem jest półton. Ta skala jest równocześnie i dur i mol. Skala ta daje niebywale oryginalne możliwości harmonizacji. Grając w tonacji E możemy mieć jako akord toniczny: E-dur albo Em albo … Edim7. Dalej jest jeszcze zabawniej.
2. Skala durowa harmoniczna jest odwróceniem skali molowej harmonicznej (jak widać z obrazka). Tu przyznaje się do kompletnej ignorancji – nie grałem tego ani chyba też żadnego modusa tej skali.
3. Odwróceniem skali węgierskiej durowej jest skala rumuńska durowa. Jak wyżej – jestem tu kompletnym ignorantem ale ciesze się, że dzięki zabawie w kombinatorykę muzyczną udało się tu dotrzeć. Temat do zbadania i opisania.

Razem mamy więc 6 rodzajów skal * 7 modusów każda co daje 42 skale z których każda może występować w 12 tonacjach. Razem 504 „gamy” do przećwiczenia. Czego Wszystkim i sobie życzę!